This thesis details an approach known as change-point detection (CPD) that aims to detect changes in the mean, variance and covariance of a time series. The scope of CPD is limited to an on-line (real-time) Bayesian spatio-temporal setting. In this setting, the goal of CPD is to provide step-ahead predictions and partition the time series into disjoint segments every time a new datum is received using Bayesian inference. This is achieved by modelling each datum as a sample from a data-generating process which we are imitating using a probability distribution as a model. At each time step the most likely model is chosen among a universe of potential models. This leads to the development of the Bayesian on-line change-point detection and model selection (BOCDMS) algorithm which has a linear computational and storage complexity in the number of observations.

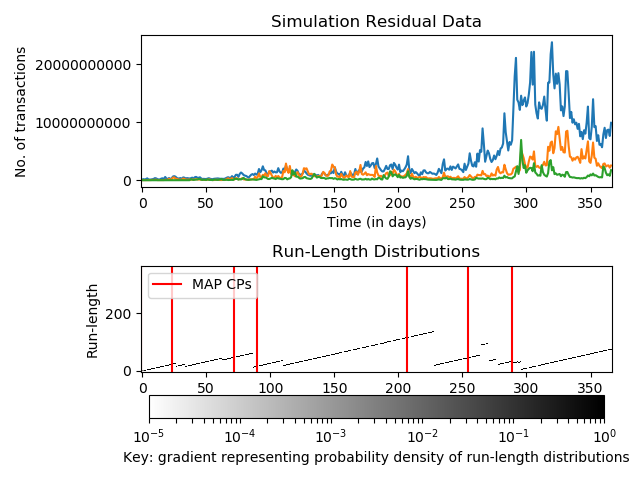
Model selection is narrowed by employing two conjugate point process models: the Poisson Gamma (PG) and Multinomial Dirichlet (MD) models. We study the properties of these models and assess their sensitivity and performance on four synthetic and three real-world datasets, the latter of which are related to crime in Chicago, property transactions in the UK and cryptocurrency transactions.